Eluer-Maclaurin求和公式

0.

在这里不想讨论公式本身，这里是求和公式的wikipedia页面

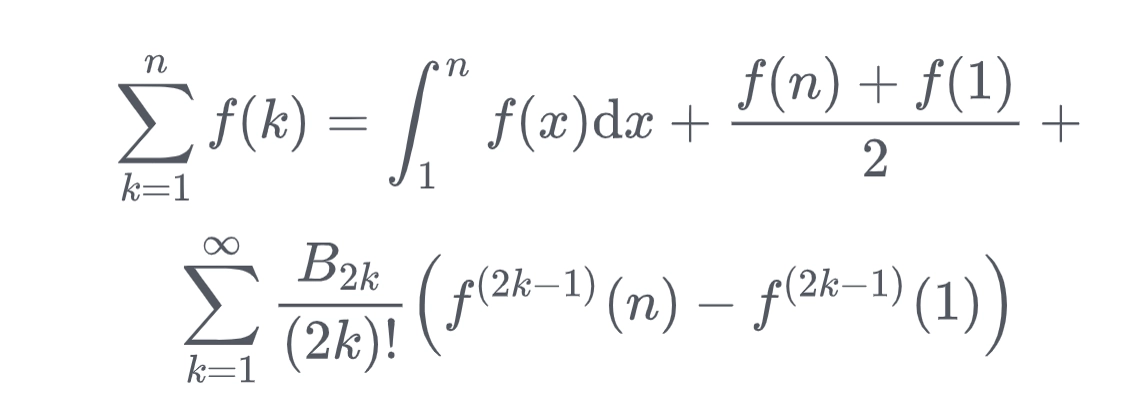
1.简单推导

1.0直觉

这一公式的基本思路在于将离散的差分转为连续的求导。 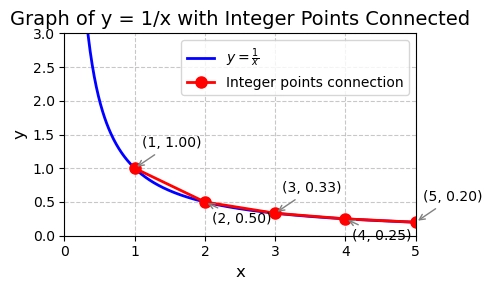从这张图就能看出，梯形积分和不规则梯形积分的差别是较小的。

1.1 正式推导

引入微分算子 和差分算子

由 Taylor 公式

可以得到

这里推导 和 的关系：
我们知道

所以

差分算子求和不具有交换性，不能直接拆括号，这里应该理解为
所以：

转换成连续形式：

注意到：

引入伯努利级数的母函数：

因此

展开得：

最终得到：

Q.E.D.